Materialparametrene som foreslås for stål er:

• Elastisitetsmodul: E = 210 000 N/mm²
• Skjærmodul: G = 81 000 N/mm² (80 000 N/mm² i NS 3472)
• Tyngdetetthet: r = 77 kN/m³
• Varmeutvidelseskoeffisient: a = 1.2·10^-5 K^-1

I Focus Konstruksjon kan man velge mellom 14 fasthetsklasser. Den foreslåtte fasthetsklassen er S355. Man kan også velge egendefinert stålkvalitet, hvor flytespenningene oppgis av bruker.

Dimensjonerende materialfasthet f_d er gitt som en karakteristisk fasthet (flytespenning) dividert med materialkoeffisient:

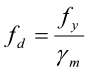
Flytespenningen f_y avhenger av stålkvaliteten og av tverrsnittets form (godstykkelse). Se tabell i standarden. Materialfaktoren g_m er avhengig av hvilken kontroll som utføres. For påvisning av tverrsnittskapasitet skal materialfaktoren settes lik g_M0 = 1.00, og for beregning av stavknekking skal materialfaktoren settes lik g_M1 = 1.00. (I NS 3472 brukes g_M1 = 1.10 i begge tilfellene.)

Det er to måter å dimensjonere et ståltverrsnitt på: elastisk dimensjonering og plastisk dimensjonering. Elastisk dimensjonering tillater flytning i mest påkjente punkt i tverrsnittet, mens plastisk dimensjonering tillater at hele tverrsnittet flyter. Det sier seg da selv at den plastiske kapasiteten til et tverrsnitt alltid er større enn den elastiske, forutsatt at tverrsnittet lar seg dimensjonere etter plastisitetsteori. Det er tverrsnittsklassen som avgjør hvilke dimensjoneringsmetoder som er tillatt. Tverrsnittsklassen til et tverrsnitt er bestemt av tverrsnittets dimensjoner (slankhet) og belastningssituasjon. For åpne tverrsnitt bestemmes tverrsnittsklassen til de enkelte tverrsnittskomponentene hver for seg, og tverrsnittets klasse er lik den laveste av de enkelte komponentenes klasser. Tverrsnittsklasse for forskjellige tverrsnitt og tverrsnittsdeler er listet opp i standarden. De tre tverrsnittsklassene som er aktuelle i Focus Konstruksjon, er klasse 2, klasse 3 og klasse 4. Klasse 1, som tillater bruk av flyteleddsmetoder med full rotasjon, dvs. omfordeling av krefter i konstruksjonen, er med dagens beregningsmetode i Focus Konstruksjon (tverrsnittskreftene bestemmes med antagelse om lineært elastiske materialer) umulig å utnytte. Tverrsnittsklasse 2 tillater at tverrsnittet dimensjoneres etter plastisitetsteori, mens tverrsnitt med tverrsnittsklasse 3 bare kan dimensjoneres etter elastisitetsteori. Tverrsnitt med tverrsnittsklasse 4 får lokal knekning for en spenning som er lavere enn flytespenningen i mest påkjente fiber, og krever spesiell beregning. I disse tilfellene regner programmet ut et effektivt tverrsnitt hvor de knekningsutsatte delene av tverrsnittet er tatt bort. Kapasitetsutnyttelsen beregnes da for det effektive tverrsnittet. Kapasitetskontroll i tverrsnittsklasse 4 er bare tilgjengelig hvis man bruker Eurokode; hvis man bruker Norsk Standard blir disse tverrsnittene ikke kontrollert (de blir hvite i kapasitetskartet).

Stabilitet

I stabilitetskontrollen for stål spiller momentvariasjon langs bjelken/søylen en stor rolle. Programmet baserer seg på at det er entydige sammenhenger mellom segmentene og de fysiske konstruksjonselementene. Hvis en bjelke/søyle i Focus Konstruksjon blir delt opp i to eller flere segmenter, har programmet ingen mulighet til å finne endekreftene eller momentforløpet til bjelken/søylen. Dette kan gi resultater til usikker side i stabilitetskontrollen..

Lokale effekter

Focus Konstruksjon tar ikke hensyn til lokale spenningsforhøyelser rundt innføring av punktlast og opplegg. For eksempel er hatteprofil ofte belastet på de utstikkende flensene, og dette skaper moment og dermed bøyespenninger på tvers av bjelkeaksen:

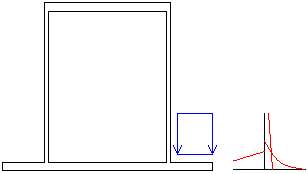
Figuren til venstre viser belastning av hatteprofilets flens, og figuren til høyre viser bøyemomentet som denne belastningen gir i nedre høyre del av tverrsnittet. Bøyemomentet gir bøyespenninger på tvers av bjelkeaksen som Focus Konstruksjon ikke tar hensyn til; de må kontrolleres manuelt.

Hvelvningstorsjon

Focus Konstruksjon tar ikke hensyn til hvelvningstorsjon. Denne effekten oppstår i torsjonsbelastede tverrsnitt som ikke er hvelvningsfrie og som er innspent slik at hvelvning er forhindret. Aksialspenningene i torsjonspåkjente I-profiler, kanalprofiler og hatteprofiler kan derfor være underestimert.

Her er en oversikt over hva som kontrolleres for stål i de forskjellige grensetilstandene.

Bruddgrensetilstanden

Dimensjonskontrollene er organisert i én tverrsnittskontroll og én stabilitetskontroll. Konstruksjonen kan dimensjoneres etter elastisitetsteori eller plastisitetsteori (hvis tverrsnittsklassen tillater det).

Ulykkesgrensetilstanden

Ulykkesgrensetilstanden er i Focus Konstruksjon ensbetydende med brann. Ulykkesgrensetilstanden kontrolleres i hovedsak som bruddgrensetilstanden, men med følgende modifikasjoner:

Når man regner i grensetilstand brann tas det hensyn til at flytespenning og elastisitetsmodul reduseres når temperaturen øker. Standardene EN 1993 og NS 3472 angir i tabeller hvordan f_y og E reduseres med temperaturen. Skjærmodulen G reduseres i Focus Konstruksjon på samme måte som E.

I tillegg til reduksjon av flytespenning og E-modul angir standardene enkelte modifikasjoner i forhold til formlene og metodene som benyttes i bruddgrensetilstanden.

Materialkoeffisienten g_m for stål blir av programmet automatisk satt lik 1.0 før beregning i ulykkesgrensetilstanden.

Bruksgrensetilstanden

I bruksgrensetilstanden skal konstruksjonen kontrolleres for

• deformasjoner som har betydning for den normale bruk av konstruksjonen eller byggverket
• vibrasjoner eller svingninger som gir ubehag eller påvirker bruk av konstruksjonen eller byggverket
• lokale skader som har betydning for konstruksjonens eller byggverkets levetid

Focus Konstruksjon er behjelpelig med bare den første av disse tre kontrollene. Programmet beregner forskyvningene, men brukeren må selv kontrollere om deformasjonene er akseptable. Kapasitetsutnyttelse kan beregnes også i bruksgrensetilstanden, men da er bare elastisk beregning tillatt. Materialkoeffisienten g_m for stål blir av programmet automatisk satt lik 1.0 før beregning i bruksgrensetilstanden.

Et tverrsnitts elastiske kapasitet er bestemt ved initiell flytning i det mest påkjente punkt i tverrsnittet. Etter von Mises’ teori oppstår flytning når jevnføringsspenningen s_j blir lik dimensjonerende flytespenning f_d. Dimensjoneringskravet i elastisitetsteorien er derfor

Jevnføringsspenningen beregnes etter formelen

.

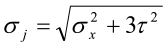Komponentene i s_j er

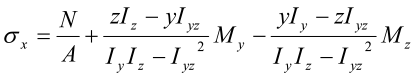
Her er S^’_y og S^’_z statisk moment (første arealmoment) om hhv. y-aksen og z-aksen for den delen av tverrsnittet som ligger ”utenfor” snittet vi betrakter, og t er tykkelsen av tverrsnittet i det betraktede snitt.

Jevnføringsspenningen skal være innenfor tillatt grense i hele tverrsnittet. Siden vi kjenner fordelingen av spenningene over tverrsnittet, kan vi plukke ut noen få punkter hvor jevnføringsspenningen kan ha sin maksimale verdi, og beregne den i hvert av disse punktene. Dette har vi gjort, og hver tverrsnittsform har et eget sett med punkter hvor jevnføringsspenningen sjekkes.

Kontroll mot jevnføringsspenning gjelder kun dersom tverrsnittsklassen er 3 eller mindre. I tverrsnittsklasse 4 brukes i stedet formel (6.44) i EN 1993-1-1:

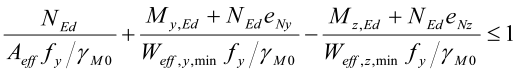
Mens elastisitetsteorien tillater flytning kun i mest påkjente fiber, tillater plastisitetsteorien at hele tverrsnittet flyter.

Den plastiske tverrsnittskontrollen utføres etter NS 3472 pkt. 12.2.3 – 12.2.8.

Aksialkraft

For normalkraft gjelder:

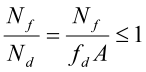
Moment

For moment om én akse gjelder:

For biaksialt moment beregnes kapasiteten som

hvor a og b er tverrsnittsavhengige eksponenter gitt i NS3472/3 Tabell 9.

Skjærkraft

For skjærkraft gjelder:

A_v er skjærarealet. Skjærknekking (12.4.4) tas ikke hensyn til.

Moment og aksialkraft

Ved samtidig moment og aksialkraft reduseres momentkapasiteten:

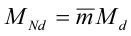
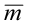er reduksjonsfaktor på grunn av aksialkraft, for den relevante bøyningsaksen. Denne faktoren er avhengig av tverrsnittsformen. Kapasitetsutnyttelsen beregnes som

hvor a og b er tverrsnittsavhengige eksponenter gitt i NS3472/3 Tabell 9.

Moment og skjærkraft

Skjærkraftens innvirkning på momentkapasiteten neglisjeres dersom

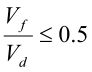
For større skjærkrefter regnes det med en redusert flytespenning f_d,V i tverrsnittets skjærareal:

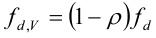
hvor

Vi kaller skjærarealets reduserte motstandsmoment for W_p,V og finner tverrsnittets reduserte momentkapasitet M_Vd:

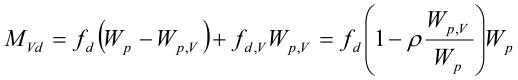
Kapasitetsutnyttelsen er lik den største av

og

hvor a og b er tverrsnittsavhengige eksponenter gitt i NS3472/3 Tabell 9.

Moment, aksialkraft og skjærkraft

Hvis

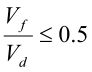
dimensjoneres tverrsnittet for moment og aksialkraft, uten hensyn til skjærkraften.

For større skjærkrefter er den reduserte momentkapasiteten lik

hvor M_d,N er tverrsnittets momentkapasitet redusert for aksialkraft, uten hensyn til skjærkraften. M_d,fl er momentkapasiteten av flensene alene.

Med denne reduserte momentkapasiteten beregnes kapasiteten forøvrig som for kombinasjonen av moment og aksialkraft (NS 3472/3 12.2.6).

Mens elastisitetsteorien tillater flytning kun i mest påkjente fiber, tillater plastisitetsteorien at hele tverrsnittet flyter.

Den plastiske tverrsnittskontrollen utføres etter EN 1993-1-1 pkt. 6.2.3 – 6.2.10.

Aksialkraft

For aksialkraft gjelder:

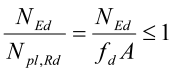
Moment

For moment om én akse gjelder:

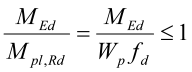
For biaksialt moment beregnes kapasiteten som

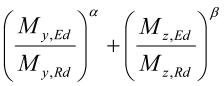
hvor a og b er tverrsnittsavhengige eksponenter gitt i EN 1993-1-1 6.2.9.1 (6).

Skjærkraft

For skjærkraft gjelder:

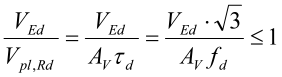
A_v er skjærarealet. Skjærknekking tas ikke hensyn til.

Torsjon

For torsjon gjelder:

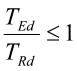
Som tidligere nevnt, blir ikke hvelvningstorsjon tatt hensyn til.

Torsjon og skjærkraft

Torsjon reduserer skjærkraftkapasiteten fra V_pl,Rd til V_pl,T,Rd som beskrevet i EN 1993-1-1 6.2.7 (9).

Moment og skjærkraft

Skjærkraftens innvirkning på momentkapasiteten neglisjeres dersom

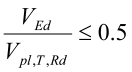
For større skjærkrefter regnes det med en redusert flytespenning f_d,V i tverrsnittets skjærareal:

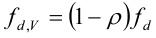
hvor

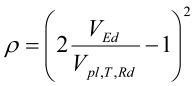
Her er skjærkraftkapasiteten redusert for torsjon (hvis torsjon er til stede). Den reduserte flytespenningen gir opphav til reduserte momentkapasiteter. Vi kaller skjærarealets reduserte motstandsmoment for W_p,V og finner tverrsnittets reduserte momentkapasitet M_V,Rd:

Kapasitetsutnyttelsen er lik den største av

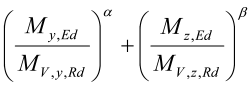og

hvor a og b er tverrsnittsavhengige eksponenter gitt i EN 1993-1-1 6.2.9.1 (6).

Moment og aksialkraft

Ved samtidig moment og aksialkraft reduseres momentkapasiteten fra M_pl,Rd til M_N,Rd som beskrevet i EN 1993-1-1 6.2.9.1. Hvor mye momentkapasiteten reduseres, er avhengig av tverrsnittsformen. Kapasitetsutnyttelsen beregnes som

hvor a og b er tverrsnittsavhengige eksponenter gitt i EN 1993-1-1 6.2.9.1 (6).

Moment, aksialkraft og skjærkraft

Hvis

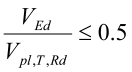
dimensjoneres tverrsnittet for bøyemoment og aksialkraft, uten hensyn til skjærkraften.

For større skjærkrefter regnes det med en redusert flytespenning f_d,V i tverrsnittets skjærareal, som beskrevet i avsnittet for moment og skjærkraft. Med denne reduksjonen av flytespenningen, beregnes kapasiteten som for kombinasjonen av moment og aksialkraft.

Stabilitetskontrollen utføres etter punkt 12.3 i NS 3472.

Konstruksjonsdeler belastet med aksialtrykk og moment skal tilfredsstille kapasitetskravet

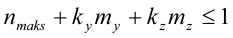
hvor k_y og k_z er momentkorreksjonsfaktorer (mer om disse nedenfor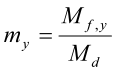), og

og 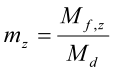er normaliserte momenter.

Videre er

,    

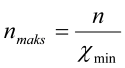hvor c_min er den minste av knekkfaktorene c_y og c_z for knekking om henholdsvis y-aksen og z-aksen.

For staver med konstant aksialkraft og konstant tverrsnitt er c_i (i = y, z) gitt som en funksjon av den relative slankhet:

der f_ki er knekkspenningen for den gitte aksen og

a er ekvivalent formfeilsfaktor fra tabell 10 i NS 3472. Den relative slankheten er

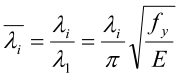hvor absolutt slankhet l er .

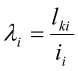Momentkorreksjonsfaktorene k_y og k_z er gitt av

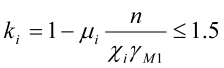
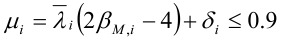
b_M,i er ekvivalent momentfaktor og gitt i standardens tabell 12.

Hvis ikke vipping er forhindret, skal konstruksjonsdelen også tilfredsstille følgende kapasitetskrav:

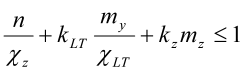
med

b_M,LT er gitt i standardens tabell 12, og c_LT er vippingsfaktoren:

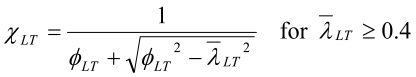
med

a_LT er ekvivalent formfeilsfaktor; verdien er 0.21 for valseprofiler og 0.49 for sveiste profiler. Den relative vippeslankheten er

M_cr er det lineariserte elastiske vippemomentet, og defineres i punkt B.12.3.4:

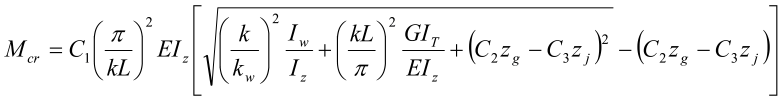
Faktorene k, k_w, C₁, C₂ og C₃ er gitt i tabellene B.3 og B.4. Høyden z_g er avstanden mellom lastangrepspunkt og skjærsenter:

z_j er definert ved

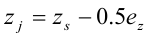
der

Stabilitetskontrollen utføres etter punkt 6.3 i EN 1993.

Konstruksjonsdeler belastet med aksialtrykk og moment skal tilfredsstille kapasitetskravene gitt i ligning (6.61) og (6.62):

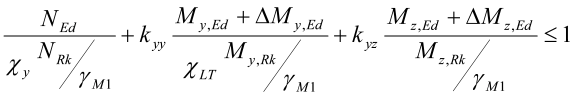
hvor k_yy , k_yz, k_zy og k_zz er interaksjonsfaktorer gitt i standardens tillegg B. ΔM_y,Ed og ΔM_z,Ed er momenter på grunn av flytting av nøytralaksen i tverrsnittsklasse 4. Dersom tverrsnittsklassen er mindre enn 4, er disse momentene lik null.

For staver med konstant aksialkraft og konstant tverrsnitt er knekkfaktoren c_i (i = y, z) gitt som en funksjon av den relative slankhet:

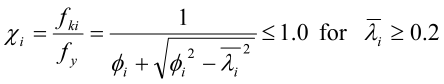
der f_ki er knekkspenningen for den gitte aksen og

a er ekvivalent formfeilsfaktor fra tabell 6.1 i EN 1993-1-1. Den relative slankheten er

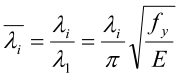hvor absolutt slankhet l er .

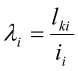Hvis ikke vipping er forhindret, skal konstruksjonsdelen også tilfredsstille følgende kapasitetskrav:

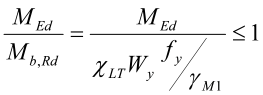
hvor

• Wy = Wpl,y for tverrsnitt i klasse 1 eller 2
• Wy = Wel,y for tverrsnitt i klasse 3
• Wy = Weff,y for tverrsnitt i klasse 4.

c_LT er vippingsfaktoren:

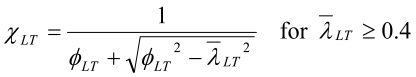
med

a_LT er ekvivalent formfeilsfaktor hvor verdien tas fra EN 1993-1-1 Tabell 6.3. Den relative vippeslankheten er

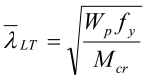
M_cr er det lineariserte elastiske vippemomentet. Eurokode 3 gir ingen informasjon om hvordan M_cr skal bestemmes, så vi bruker fremgangsmåten gitt i NS 3472, 3. utgave 2001, punkt B.12.3.4:

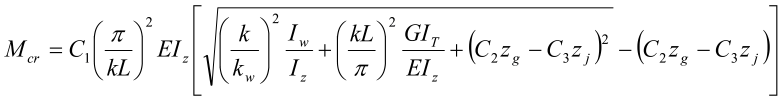
Faktorene k, k_w, C₁, C₂ og C₃ er gitt i tabellene B.3 og B.4 i NS 3472. Høyden z_g er avstanden mellom lastangrepspunkt og skjærsenter:

z_j er definert ved

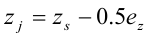
der

For skall utføres elastisk spenningskontroll i henhold til EN 1993-1-6 punkt 6.2.3:

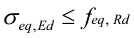
Kapasitetskontroll for skall er ikke tilgjengelig dersom man bruker Norsk Standard.

Siden aksialkraften N er den eneste størrelsen i stabilitetskontrollen som kan variere langs segmentene, vil stabilitetskontrollen for stål etter NS 3472 i Focus Konstruksjon vanligvis gi konstant utnyttelse i hele segmentet.

Stabilitetsutnyttelsen for stål i Focus Konstruksjon blir større enn null selv om brukeren setter knekk- og vippelengder lik null. Det kommer av utformingen av formlene for knekning, der det momentet divideres med momentkapasitet for hhv. bøyning og vipping. Momentkapasiteten for bøyning er uavhengig av knekklengde, og momentkapasiteten for vipping blir aldri større enn momentkapasiteten for bøyning.